上一篇：六角星形數字之排列（上）

（八）合於條件排列之變形

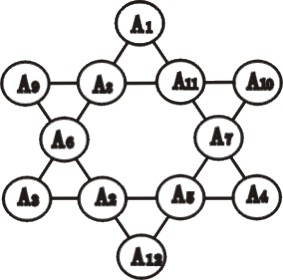
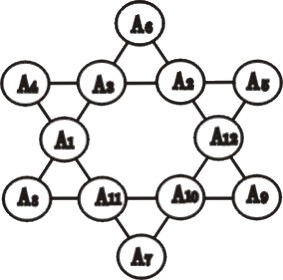
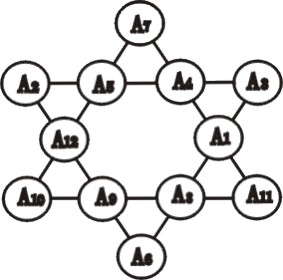
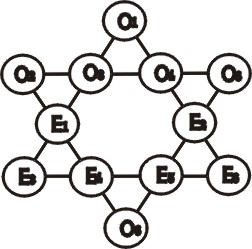
（1）將合於條件之排列（如圖二）中一邊上四數與其平行邊上四數相互交叉調換，則所得之新排列仍合於條件。因在各邊上四數經變動後，仍在同一邊上，其和仍為 26 未變。由於星形包含三組平行邊，故合於條件之排列共有三個變形，如圖四、圖五及圖六所示，稱之為變形一、變形二及變形三。

（2）合於條件之排列，尚有另一類變形。

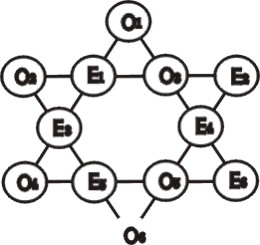
將合於條件之排列（如圖二）中各 A_i 換為 B_i＝13 – A_i，_i＝1 至 12，則所得之排列所示亦合於條件，因若 A_m，A_n，A_j 及 A_k 為圖二排列中任一邊上四數（其和為 26）經變換後，該邊上四數為 B_m，B_n，B_j 及 B_k 則：

B_m＋B_n＋B_j＋B_k＝（13 – A_m）＋（13 – A_n）

＋（13 – A_j）＋（13 – A_k）

＝52 –（A_m＋A_n＋A_j＋A_k）
＝52 – 26＝26

即變換後每邊上四數之和仍為 26，且 B_i，_i＝1 至 12 亦為 1 至 12 諸數之組合，故所得之新排列合於條件。

但當 A₁＋A₆＝13 或 A₁＋A₇＝13 時，經此種變形後其一型（二型）菱形上四數未變，僅位置易動變成二型（一型）而已。所得結果與前類變型相同。

（3）如將合於條件之排列，依垂直紙面任一直線為軸旋轉 60 度或 60 度之倍數，或依紙面上任一直線為軸旋轉 180 度所得之排列當然仍合於條件，因數與數間相對位置沒有變動，實為同一種排列，似不應視為新解，如不予列舉。因此，為便於辨認比較，玆選取中間豎立之菱形為第一型或第二型為標準形，即中間豎立之菱形為第一或第二型，且其上方數字較下方數字為小。而左邊數字較右邊數字為小，以下將以此等標準形式作為研討之對象。

綜合以上所得可推出尋找合於條件排列之捷徑如下：

（一）圖八型合於條件排列之尋求。

（1）選定第一型菱形上四數：首先在 1 至 12 等數中取出兩奇數，而使剩餘四奇數可均分為相等之兩組數（即符合性質五）。此兩數計有以下七個組合：

（1, 3）（1, 7）（1, 11）（3, 9）（5, 7）（5, 11）（9, 11）

然後再取出兩偶數，亦使剩餘四偶數能均分為相等之兩組數。此組合亦有七組如下：

（2, 4）（2, 8）（2, 12）（4, 10）（6, 8）（6, 12）（10, 12）

在以上兩組數中，配成總和為 26 之組合計有 13 組如下：

（1, 3）（10, 12）；（1, 7）（6, 12）；（1, 11）（2, 12）；
（1, 11）（6, 8）；（3, 9）（ 2, 12）；（3, 9）（4, 10）；
（3, 9）（6, 8）；（5, 7）（2, 12）；（5, 7）（4, 10）；
（5, 7）（6, 8）；（5, 11）（2, 8）；（9, 11）（2, 4）；
（1, 11）（4, 10）。

以上每一組合均可用作第一型菱形上四數，可依順序一一加以測試。

首先取第一組｛（1, 3）（10, 12）｝四數放置在第一型菱形上如圖九所示。

（2）計算出第一型菱形上每邊已放置之兩數和

第一邊 3＋10＝13（X₃）；第二邊 1＋10＝11（X₄）
第三邊 1＋12＝13（X₁）；第四邊 3＋12＝15（X₂）

由性質五知 13（X₁），15（X₂），13（X₃），11（X₄）分別第 1 至 4 邊上應填入一奇一偶之和（如此第 1 至 4 邊上四數之和均為 26）。

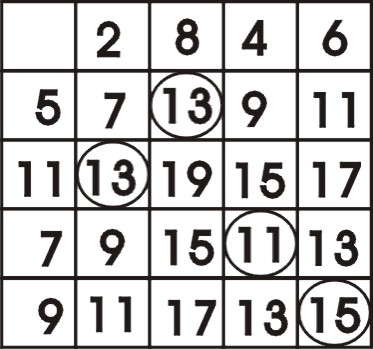
（3）將剩餘之奇數平分（5，11）（7，9）及剩餘之偶數平分（2，8）（4，6）後，一對一相加並將結果依序列出如附表一。依下列兩條件找出與 X₁，X₂，X₃ 及 X₄ 相同之四數：

（1）四數分屬於不同之行與列（即此四數之組成數為全部剩餘之奇數及偶數，無重複）；

（2）與 X₁，X₃ 相同之兩數在同一 2×2 分方塊中，而與 X₂，X₄ 相同之兩數，則在不相鄰之另一 2×2 分方塊中（如此第 5 及 6 邊上四數分由等分之剩餘奇數組及偶數組各一組所組成，其和均為 26）。

合以上兩條件之四數及其組成數如下：

X₁：13＝5＋8；X₃：13＝11＋2；X₂：15＝6＋9；X₄：11＝4＋7

[下一篇：六角星形數字之排列（下）]