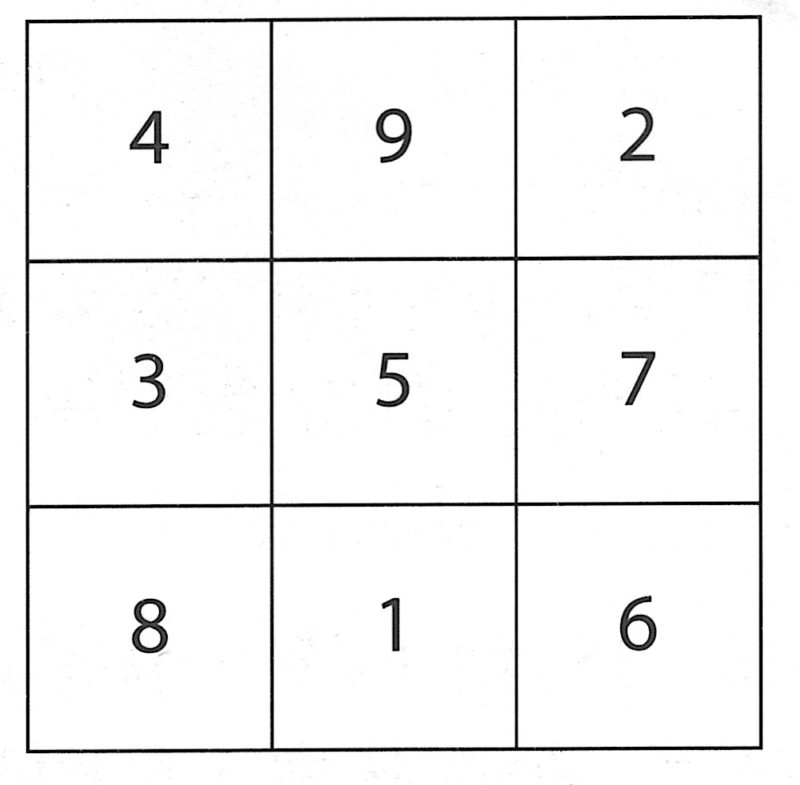
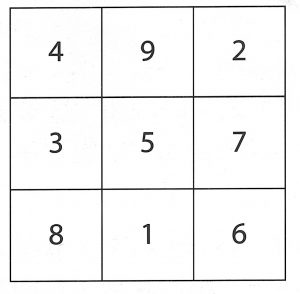
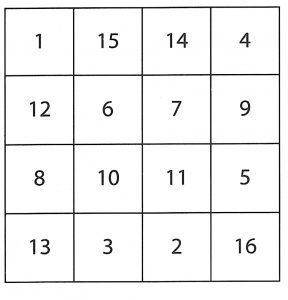
魔方是甚麼?下面兩個圖形就分別是三階和四階的魔方:
三階魔方裡的數字,是從 1 到 9 的連續數。四階魔方裡的數字,是從 1 到 16 的連續數。三階中,直的每行,橫的每列,以及斜的對角線上的各三個數字,其和都是 15。同樣,在四階中,各四個數字的和都是 34。
若用文字表述,則可說:
魔方是用若干個小正方形,堆疊成一個大正方形,然後在每一個小正方形中,填進去若干個連續數中的一個數字,而要使直的每行,橫的每列,以及斜的對角線上的各數字的和皆相等。根據這個定義,五階、六階以致任何階的魔方,都不難想像是怎麼一回事了。
至於這各階魔方的每行(或列或對角線)各數之和是怎樣求得的呢?以三階為例,三階魔方中各連續數之和:
S3 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
因為這些連續數分據三行(或列),而各行之和又相等,故每行之和為 L3 = S3 / 3 = 15,
同理 S4 = 1 + 2 + 3 + … 16 = 136
而 L4 = S4 / 4 = 136 / 4 = 34
一般言之,用等差級數求和的公式則更為方便迅速,其公式如下:
S ( 各連續數之和 ) = ( 首項 + 末項 / 2 ) x 項數
在三階中,首項 = 1,末項 = 9,項數 = 9
故 S3 = ( 1 + 9 / 2 ) x 9 = 45,L3 = S3 / 3 = 45 / 3 = 15 同理
S4 = ( 1 + 16 / 2 ) x 16 = 136,L4 = S4 / 4 = 136 / 4 = 34
這三階魔方,大概很多人都以前見過。四階的魔方,也究屬簡單,都可以慢慢地拼湊得出來。但五階或五階以上,就麻煩多了。假若沒有一套簡單有效的方法,而想靠拼湊,幾乎是不可能的事。讀者不妨試一試,如果你在一天之內,能湊出五、六階魔方,那你可稱得是幸運的天才了。因為很多人都會徒勞無功,所以我並不鼓勵讀者去浪費時間。下面我介紹前面提到的簡單有效的方法如下:
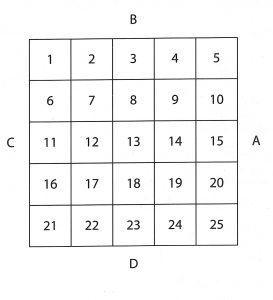
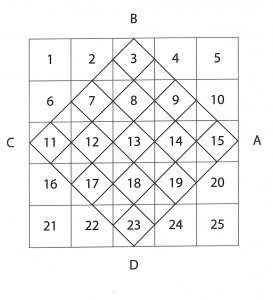
假如你現在想作一個五階的魔方,第一步先畫一個大四方形,再把它分為二十五個小正方形,然後將 1 至 25 的 25 個連續數字,依次填入 25 個方格中,如圖三。
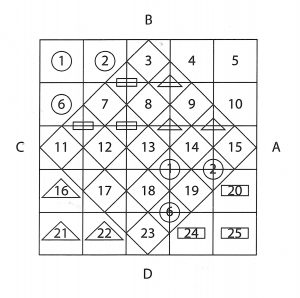
第二步,連結四邊形的四個中點 A、B、C、D,作成一個較小的正方形。再將此一較小的正方形,也分成 25 個更小的正方形,如圖四。現在可以發現原來的 25 個數字,有 13 個在新成的小正方形內,另外 12 個則在 A B C D 之外的大四方形的四個角落上。而 A B C D 之內,則有 12 個空格,沒有數字。
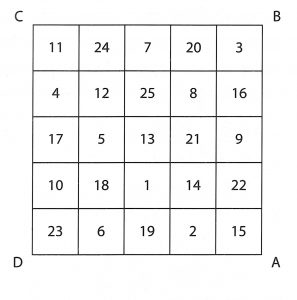
第三步,參看圖五,將大四方形左上角圓圈內的數字 1、2、6,移入小四方形 A、B、C、D 內有圓圈的位置。左下角三角形內數字的數字 16、21、22 移入 A、B、C、D 內有三角形的位置,右下角長方形內的數字 20、24、25 移入 A、B、C、D 內有長方形的空格,剩下的 4、5、10 也倣照前面的移法移入,就成了圖六的五階魔方。
這魔方內的數字為 1 到 25 的 25 個連續數。
其首項 = 1 末項 = 25 項數 = 25
而此 25 個連續數之和 S5 = ( 1 + 25 / 2 ) x 25 = 325,
而每行(或每列)5 數字之和 L5 = 325 / 5 = 65
其餘各奇(單數)數魔方,皆可按此法求得。只不過越大越麻煩而已,至於偶數(2、4、6、8、…)魔方,就不像奇階魔那麼簡單了。容待下次再說吧。[下一篇:魔方(續):專論四階魔方]